| |
|

|
|
|
|
| |
|

|
| |
 |
NOT Gate
|
|
|
The NOT gate performs the basic logical function called inversion or complementation. NOT gate is also called inverter. The purpose of this gate is to convert one logic level into the opposite logic level. It has one input and one output. When a HIGH level is applied to an inverter, a LOW level appears on its output and vice versa. |
| |
|

|
|
|
If X is the input, then output F can be represented mathematically as F = X', Here apostrophe (') denotes the NOT (inversion) operation. There are a couple of other ways to represent inversion, F= !X, here ! represents inversion. Truth table and NOT gate symbol is shown in the figure below. |
| |
|

|
|
|
Symbol |
| |
|

|
|
|
 |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
| |
|

|
|
|
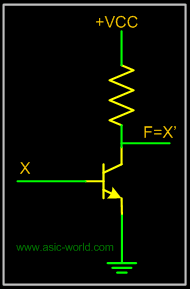
NOT gate using "transistor-resistor" logic is shown in the figure below, where X is the input and F is the output. |
| |
|

|
|
|
Circuit |
| |
|

|
|
|
 |
| |
|

|
|
|
When X = 1, The transistor input pin 1 is HIGH, this produces the forward bias across the emitter base junction and so the transistor conducts. As the collector current flows, the voltage drop across RL increases and hence F is LOW. |
| |
|

|
|
|
When X = 0, the transistor input pin 2 is LOW: this produces no bias voltage across the transistor base emitter junction. Thus Voltage at F is HIGH. |
| |
|

|
| |
 |
BUF Gate
|
|
|
Buffer or BUF is also a gate with the exception that it does not perform any logical operation on its input. Buffers just pass input to output. Buffers are used to increase the drive strength or sometime just to introduce delay. We will look at this in detail later. |
| |
|

|
|
|
If X is the input, then output F can be represented mathematically as F = X. Truth table and symbol of the Buffer gate is shown in the figure below. |
| |
|

|
|
|
Symbol |
| |
|

|
|
|
 |
| |
|

|
|
|
Truth Table |
|
|
|
| |
|

|
|
|
|
| |
|

|
| |
 |
NAND Gate
|
|
|
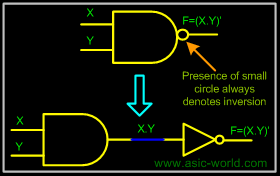
NAND gate is a cascade of AND gate and NOT gate, as shown in the figure below. It has two or more inputs and only one output. The output of NAND gate is HIGH when any one of its input is LOW (i.e. even if one input is LOW, Output will be HIGH). |
| |
|

|
|
|
NAND From AND and NOT |
| |
|

|
|
|
 |
| |
|

|
|
|
If X and Y are two inputs, then output F can be represented mathematically as F = (X.Y)', Here dot (.) denotes the AND operation and (') denotes inversion. Truth table and symbol of the N AND gate is shown in the figure below. |
| |
|

|
|
|
Symbol |
| |
|

|
|
|
 |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
X
|
Y
|
F=(X.Y)'
|
|
0
|
0
|
1
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
|
| |
|

|
| |
 |
NOR Gate
|
|
|
NOR gate is a cascade of OR gate and NOT gate, as shown in the figure below. It has two or more inputs and only one output. The output of NOR gate is HIGH when any all its inputs are LOW (i.e. even if one input is HIGH, output will be LOW). |
| |
|

|
|
|
Symbol |
| |
|

|
|
|
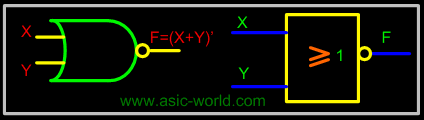 |
| |
|

|
|
|
If X and Y are two inputs, then output F can be represented mathematically as F = (X+Y)'; here plus (+) denotes the OR operation and (') denotes inversion. Truth table and symbol of the NOR gate is shown in the figure below. |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
X
|
Y
|
F=(X+Y)'
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
0
|
|
| |
|

|
| |
 |
XOR Gate
|
|
|
An Exclusive-OR (XOR) gate is gate with two or three or more inputs and one output. The output of a two-input XOR gate assumes a HIGH state if one and only one input assumes a HIGH state. This is equivalent to saying that the output is HIGH if either input X or input Y is HIGH exclusively, and LOW when both are 1 or 0 simultaneously. |
| |
|

|
|
|
If X and Y are two inputs, then output F can be represented mathematically as F = X Y, Here Y, Here 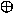 denotes the XOR operation. X denotes the XOR operation. X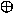 Y and is equivalent to X.Y' + X'.Y. Truth table and symbol of the XOR gate is shown in the figure below. Y and is equivalent to X.Y' + X'.Y. Truth table and symbol of the XOR gate is shown in the figure below. |
| |
|

|
|
|
XOR From Simple gates |
| |
|

|
|
|
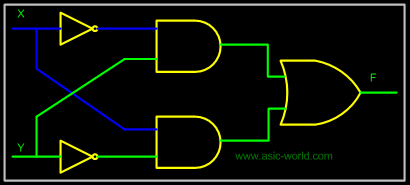 |
| |
|

|
|
|
Symbol |
| |
|

|
|
|
 |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
X
|
Y
|
F=(X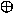 Y) Y)
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
|
| |
|

|
| |
 |
XNOR Gate
|
|
|
An Exclusive-NOR (XNOR) gate is gate with two or three or more inputs and one output. The output of a two-input XNOR gate assumes a HIGH state if all the inputs assumes same state. This is equivalent to saying that the output is HIGH if both input X and input Y is HIGH exclusively or same as input X and input Y is LOW exclusively, and LOW when both are not same. |
| |
|

|
|
|
If X and Y are two inputs, then output F can be represented mathematically as F = X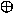 Y, Here Y, Here 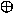 denotes the XNOR operation. X denotes the XNOR operation. X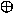 Y and is equivalent to X.Y + X'.Y'. Truth table and symbol of the XNOR gate is shown in the figure below. Y and is equivalent to X.Y + X'.Y'. Truth table and symbol of the XNOR gate is shown in the figure below. |
| |
|

|
|
|
Symbol |
| |
|

|
|
|
 |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
X
|
Y
|
F=(X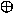 Y)' Y)'
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
|
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|