| |
|

|
|
|
|
| |
|

|
| |
 |
Symbolic Logic
|
|
|
Boolean algebra derives its name from the mathematician George Boole. Symbolic Logic uses values, variables and operations : |
| |
|

|
|
|
- True is represented by the value 1.
- False is represented by the value 0.
|
|
|
Variables are represented by letters and can have one of two values, either 0 or 1. Operations are functions of one or more variables. |
|
|
- AND is represented by X.Y
- OR is represented by X + Y
- NOT is represented by X' . Throughout this tutorial the X' form will be used and sometime !X will be used.
|
|
|
These basic operations can be combined to give expressions. |
| |
|

|
|
|
Example : |
| |
|

|
|
|
|
| |
|

|
| |
 |
Precedence
|
|
|
As with any other branch of mathematics, these operators have an order of precedence. NOT operations have the highest precedence, followed by AND operations, followed by OR operations. Brackets can be used as with other forms of algebra. e.g. |
| |
|

|
|
|
X.Y + Z and X.(Y + Z) are not the same function. |
| |
|

|
| |
 |
Function Definitions
|
|
|
The logic operations given previously are defined as follows : |
| |
|

|
|
|
Define f(X,Y) to be some function of the variables X and Y. |
| |
|

|
|
|
f(X,Y) = X.Y |
|
|
- 1 if X = 1 and Y = 1
- 0 Otherwise
|
| |
|

|
|
|
f(X,Y) = X + Y |
|
|
- 1 if X = 1 or Y = 1
- 0 Otherwise
|
| |
|

|
|
|
f(X) = X' |
|
|
|
| |
|

|
| |
 |
Truth Tables
|
|
|
Truth tables are a means of representing the results of a logic function using a table. They are constructed by defining all possible combinations of the inputs to a function, and then calculating the output for each combination in turn. For the three functions we have just defined, the truth tables are as follows. |
| |
|

|
|
|
AND |
|
|
|
X
|
Y
|
F(X,Y)
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
|
| |
|

|
|
|
OR |
|
|
|
X
|
Y
|
F(X,Y)
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
|
| |
|

|
|
|
NOT |
|
|
|
| |
|

|
|
|
Truth tables may contain as many input variables as desired |
| |
|

|
|
|
F(X,Y,Z) = X.Y + Z |
|
|
|
X
|
Y
|
Z
|
F(X,Y,Z)
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1
|
|
| |
|

|
| |
 |
Boolean Switching Algebras
|
|
|
A Boolean Switching Algebra is one which deals only with two-valued variables. Boole's general theory covers algebras which deal with variables which can hold n values. |
| |
|

|
| |
 |
Axioms
|
|
|
Consider a set S = { 0. 1} |
|
|
Consider two binary operations, + and . , and one unary operation, -- , that act on these elements. [S, ., +, --, 0, 1] is called a switching algebra that satisfies the following axioms S |
| |
|

|
| |
 |
Closure
|
| |
|

|
|
|
If X 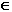 S and Y S and Y 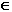 S then X.Y S then X.Y 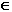 S S |
|
|
If X 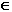 S and Y S and Y 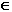 S then X+Y S then X+Y 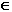 S S |
| |
|

|
| |
 |
Identity
|
| |
|

|
|
|
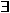 an identity 0 for + such that X + 0 = X an identity 0 for + such that X + 0 = X
|
|
|
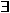 an identity 1 for . such that X . 1 = X an identity 1 for . such that X . 1 = X
|
| |
|

|
| |
 |
Commutative Laws
|
| |
|

|
|
|
X + Y = Y + X |
|
|
X . Y = Y . X |
| |
|

|
| |
 |
Distributive Laws
|
| |
|

|
|
|
X.(Y + Z ) = X.Y + X.Z |
|
|
X + Y.Z = (X + Y) . (X + Z) |
| |
|

|
| |
 |
Complement
|
| |
|

|
|
|
 X X 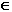 S S 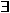 a complement X'such that a complement X'such that
|
|
|
X + X' = 1 |
|
|
X . X' = 0 |
|
|
The complement X' is unique. |
| |
|

|
|
|
|
| |
|

|
| |
 |
Theorems
|
| |
|

|
|
|
A number of theorems may be proved for switching algebras |
| |
|

|
| |
 |
Idempotent Law
|
| |
|

|
|
|
X + X = X |
|
|
X . X = X |
| |
|

|
| |
 |
DeMorgan's Law
|
| |
|

|
|
|
(X + Y)' = X' . Y', These can be proved by the use of truth tables. |
| |
|

|
|
|
Proof of (X + Y)' = X' . Y' |
| |
|

|
|
|
|
X
|
Y
|
X+Y
|
(X+Y)'
|
|
0
|
0
|
0
|
1
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
|
| |
|

|
|
|
|
X
|
Y
|
X'
|
Y'
|
X'.Y'
|
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
0
|
|
| |
|

|
|
|
The two truth tables are identical, and so the two expressions are identical. |
| |
|

|
|
|
(X.Y) = X' + Y', These can be proved by the use of truth tables. |
| |
|

|
|
|
Proof of (X.Y) = X' + Y' |
| |
|

|
|
|
|
X
|
Y
|
X.Y
|
(X.Y)'
|
|
0
|
0
|
0
|
1
|
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
|
1
|
1
|
1
|
0
|
|
| |
|

|
|
|
|
X
|
Y
|
X'
|
Y'
|
X'+Y'
|
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
1
|
|
1
|
1
|
0
|
0
|
0
|
|
| |
|

|
|
|
Note : DeMorgans Laws are applicable for any number of variables. |
| |
|

|
| |
 |
Boundedness Law
|
| |
|

|
|
|
X + 1 = 1 |
|
|
X . 0 = 0 |
| |
|

|
| |
 |
Absorption Law
|
| |
|

|
|
|
X + (X . Y) = X |
|
|
X . (X + Y ) = X |
| |
|

|
| |
 |
Elimination Law
|
| |
|

|
|
|
X + (X' . Y) = X + Y |
|
|
X.(X' + Y) = X.Y |
| |
|

|
| |
 |
Unique Complement theorem
|
| |
|

|
|
|
If X + Y = 1 and X.Y = 0 then X = Y' |
| |
|

|
| |
 |
Involution theorem
|
| |
|

|
|
|
X'' = X |
|
|
0' = 1 |
| |
|

|
| |
 |
Associative Properties
|
| |
|

|
|
|
X + (Y + Z) = (X + Y) + Z |
|
|
X . ( Y . Z ) = ( X . Y ) . Z |
| |
|

|
| |
 |
Duality Principle
|
|
|
In Boolean algebras the duality Principle can be is obtained by interchanging AND and OR operators and replacing 0's by 1's and 1's by 0's. Compare the identities on the left side with the identities on the right. |
| |
|

|
|
|
Example |
| |
|

|
|
|
X.Y+Z' = (X'+Y').Z |
| |
|

|
| |
 |
Consensus theorem
|
| |
|

|
|
|
X.Y + X'.Z + Y.Z = X.Y + X'.Z |
|
|
or dual form as below |
|
|
(X + Y).(X' + Z).(Y + Z) = (X + Y).(X' + Z) |
| |
|

|
|
|
Proof of X.Y + X'.Z + Y.Z = X.Y + X'.Z: |
| |
|

|
|
|
|
X.Y + X'.Z + Y.Z
|
= X.Y + X'.Z
|
|
X.Y + X'.Z + (X+X').Y.Z
|
= X.Y + X'.Z
|
|
X.Y.(1+Z) + X'.Z.(1+Y)
|
= X.Y + X'.Z
|
|
X.Y + X'.Z
|
= X.Y + X'.Z
|
|
| |
|

|
|
|
(X.Y'+Z).(X+Y).Z = X.Z+Y.Z instead of X.Z+Y'.Z |
|
|
X.Y'Z+X.Z+Y.Z |
|
|
(X.Y'+X+Y).Z |
|
|
(X+Y).Z |
|
|
X.Z+Y.Z |
| |
|

|
|
|
The term which is left out is called the consensus term. |
| |
|

|
|
|
Given a pair of terms for which a variable appears in one term, and its complement in the other, then the consensus term is formed by ANDing the original terms together, leaving out the selected variable and its complement. |
| |
|

|
|
|
Example : |
|
|
The consensus of X.Y and X'.Z is Y.Z |
| |
|

|
|
|
The consensus of X.Y.Z and Y'.Z'.W' is (X.Z).(Z.W') |
| |
|

|
| |
 |
Shannon Expansion Theorem
|
|
|
The Shannon Expansion Theorem is used to expand a Boolean logic function (F) in terms of (or with respect to) a Boolean variable (X), as in the following forms. |
| |
|

|
|
|
F = X . F (X = 1) + X' . F (X = 0) |
| |
|

|
|
|
where F (X = 1) represents the function F evaluated with X set equal to 1; F (X = 0) represents the function F evaluated with X set equal to 0. |
| |
|

|
|
|
Also the following function F can be expanded with respect to X, |
| |
|

|
|
|
F = X' . Y + X . Y . Z' + X' . Y' . Z |
| |
|

|
|
|
= X . (Y . Z') + X' . (Y + Y' . Z) |
| |
|

|
|
|
Thus, the function F can be split into two smaller functions. |
| |
|

|
|
|
F (X = '1') = Y . Z' |
| |
|

|
|
|
This is known as the cofactor of F with respect to X in the previous logic equation. The cofactor of F with respect to X may also be represented as F X (the cofactor of F with respect to X' is F X' ). Using the Shannon Expansion Theorem, a Boolean function may be expanded with respect to any of its variables. For example, if we expand F with respect to Y instead of X, |
| |
|

|
|
|
F = X' . Y + X . Y . Z' + X' . Y' . Z |
| |
|

|
|
|
= Y . (X' + X . Z') + Y' . (X' . Z) |
| |
|

|
|
|
A function may be expanded as many times as the number of variables it contains until the canonical form is reached. The canonical form is a unique representation for any Boolean function that uses only minterms. A minterm is a product term that contains all the variables of F¿such as X . Y' . Z). |
| |
|

|
|
|
Any Boolean function can be implemented using multiplexer blocks by representing it as a series of terms derived using the Shannon Expansion Theorem. |
| |
|

|
| |
 |
Summary of Laws And Theorms
|
| |
|

|
|
|
|
Identity
|
Dual
|
|
Operations with 0 and 1
|
|
|
X + 0 = X (identity)
|
X.1 = X
|
|
X + 1 = 1 (null element)
|
X.0 = 0
|
|
Idempotency theorem
|
|
|
X + X = X
|
X.X = X
|
|
Complementarity
|
|
|
X + X' = 1
|
X.X' = 0
|
|
Involution theorem
|
|
|
(X')' = X
|
|
|
Cummutative law
|
|
|
X + Y = Y + X
|
X.Y = Y X
|
|
Associative law
|
|
|
(X + Y) + Z = X + (Y + Z) = X + Y + Z
|
(XY)Z = X(YZ) = XYZ
|
|
Distributive law
|
|
|
X(Y + Z) = XY + XZ
|
X + (YZ) = (X + Y)(X + Z)
|
|
DeMorgan's theorem
|
|
|
(X + Y + Z + ...)' = X'Y'Z'... or { f ( X1,X2,...,Xn,0,1,+,. ) } = { f ( X1',X2',...,Xn',1,0,.,+ ) }
|
(XYZ...)' = X' + Y' + Z' + ...
|
|
Simplification theorems
|
|
|
XY + XY' = X (uniting)
|
(X + Y)(X + Y') = X
|
|
X + XY = X (absorption)
|
X(X + Y) = X
|
|
(X + Y')Y = XY (adsorption)
|
XY' + Y = X + Y
|
|
Consensus theorem
|
|
|
XY + X'Z + YZ = XY + X'Z
|
(X + Y)(X' + Z)(Y + Z) = (X + Y)(X' + Z)
|
|
Duality
|
|
|
(X + Y + Z + ...)D = XYZ... or {f(X1,X2,...,Xn,0,1,+,.)}D = f(X1,X2,...,Xn,1,0,.,+)
|
(XYZ ...)D = X + Y + Z + ...
|
|
Shannon Expansion Theorem
|
|
|
f(X1,...,Xk,...Xn)
|
Xk * f(X1,..., 1 ,...Xn) + Xk' * f(X1,..., 0 ,...Xn)
|
|
f(X1,...,Xk,...Xn)
|
[Xk + f(X1,..., 0 ,...Xn)] * [Xk' + f(X1,..., 1 ,...Xn)]
|
|
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|