|
|
| |
|

|
|
|
|
| |
|

|
| |
 |
Introduction
|
|
|
Arithmetic circuits are the ones which perform arithmetic operations like addition, subtraction, multiplication, division, parity calculation. Most of the time, designing these circuits is the same as designing muxers, encoders and decoders. |
| |
|

|
|
|
In the next few pages we will see few of these circuits in detail. |
| |
|

|
| |
 |
Adders
|
|
|
Adders are the basic building blocks of all arithmetic circuits; adders add two binary numbers and give out sum and carry as output. Basically we have two types of adders. |
| |
|

|
|
|
|
| |
|

|
|
|
|
| |
|

|
| |
 |
Half Adder
|
|
|
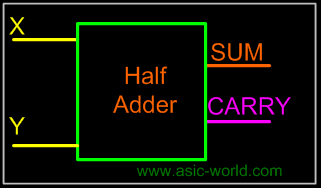
Adding two single-bit binary values X, Y produces a sum S bit and a carry out C-out bit. This operation is called half addition and the circuit to realize it is called a half adder. |
| |
|

|
|
|
Truth Table |
|
|
|
X
|
Y
|
SUM
|
CARRY
|
|
0
|
0
|
0
|
0
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
1
|
|
| |
|

|
|
|
Symbol |
| |
|

|
|
|
 |
| |
|

|
|
|
S (X,Y) = 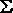 (1,2) (1,2) |
|
|
S = X'Y + XY' |
|
|
S = X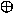 Y Y |
|
|
CARRY(X,Y) = 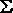 (3) (3) |
|
|
CARRY = XY |
| |
|

|
|
|
Circuit |
| |
|

|
|
|
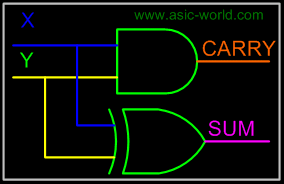 |
| |
|

|
| |
 |
Full Adder
|
|
|
Full adder takes a three-bits input. Adding two single-bit binary values X, Y with a carry input bit C-in produces a sum bit S and a carry out C-out bit. |
| |
|

|
|
|
Truth Table |
|
|
|
X
|
Y
|
Z
|
SUM
|
CARRY
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
1
|
1
|
1
|
|
| |
|

|
|
|
SUM (X,Y,Z) = 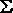 (1,2,4,7) (1,2,4,7) |
|
|
CARRY (X,Y,Z) = 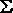 (3,5,6,7) (3,5,6,7) |
| |
|

|
|
|
Kmap-SUM |
|
|
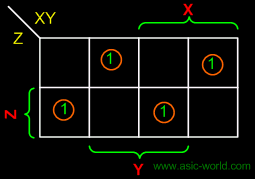 |
| |
|

|
|
|
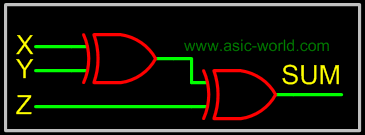
SUM = X'Y'Z + XY'Z' + X'YZ' |
|
|
SUM = X  Y Y  Z Z |
| |
|

|
|
|
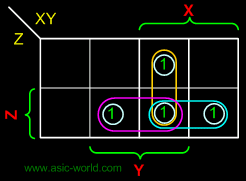
Kmap-CARRY |
|
|
 |
| |
|

|
|
|
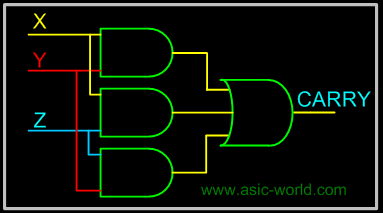
CARRY = XY + XZ + YZ |
| |
|

|
| |
 |
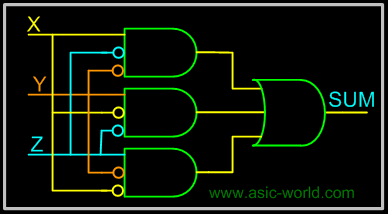
Full Adder using AND-OR
|
|
|
The below implementation shows implementing the full adder with AND-OR gates, instead of using XOR gates. The basis of the circuit below is from the above Kmap. |
| |
|

|
|
|
Circuit-SUM |
|
|
 |
| |
|

|
|
|
Circuit-CARRY |
|
|
 |
| |
|

|
| |
 |
Full Adder using AND-OR
|
| |
|

|
|
|
Circuit-SUM |
|
|
 |
| |
|

|
|
|
Circuit-CARRY |
|
|
 |
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|
|
|
|

|

|

|
|

|
|
Copyright © 1998-2025 |
Deepak Kumar Tala - All rights reserved |
|
Do you have any Comment? mail me at:deepak@asic-world.com
|
|