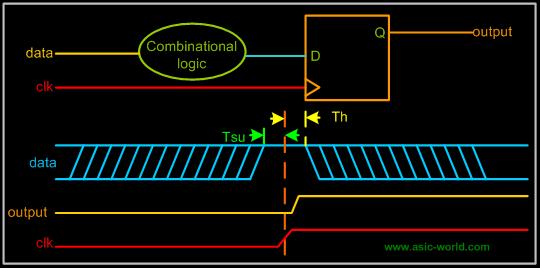
Whenever there are setup and hold time violations in any flip-flop, it enters a state where its output is unpredictable: this state is known as metastable state (quasi stable state); at the end of metastable state, the flip-flop settles down to either '1' or '0'. This whole process is known as metastability. In the figure below Tsu is the setup time and Th is the hold time. Whenever the input signal D does not meet the Tsu and Th of the given D flip-flop, metastability occurs.

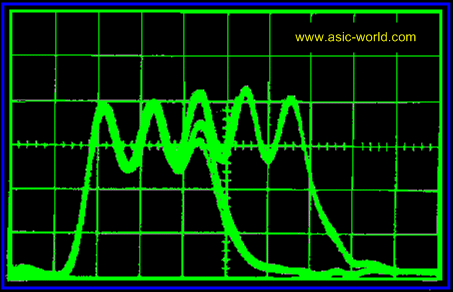
When a flip-flop is in metastable state, its output oscillate between '0' and '1' as shown in the figure below (here the flip-flop output settles down to '0') . How long it takes to settle down, depends on the technology of the flip-flop.

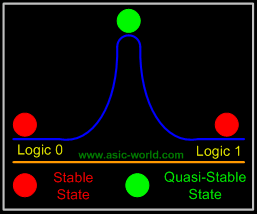
If we look deep inside of the flip-flop we see that the quasi-stable state is reached when the flip-flop setup and hold times are violated. Assuming the use of a positive edge triggered "D" type flip-flop, when the rising edge of the flip-flop clock occurs at a point in time when the D input to the flip-flop is causing its master latch to transition, the flip-flop is highly likely to end up in a quasi-stable state. This rising clock causes the master latch to try to capture its current value while the slave latch is opened allowing the Q output to follow the "latched" value of the master. The most perfectly "caught" quasi-stable state (on the very top of the hill) results in the longest time required for the flip-flop to resolve itself to one of the stable states.

The relative stability of states shown in the figure above shows that the logic 0 and logic 1 states (being at the base of the hill) are much more stable than the somewhat stable state at the top of the hill. In theory, a flip-flop in this quasi-stable hilltop state could remain there indefinitely but in reality it won't. Just as the slightest air current would eventually cause a ball on the illustrated hill to roll down one side or the other, thermal and induced noise will jostle the state of the flip-flop causing it to move from the quasi-stable state into either the logic 0 or logic 1 state.

As we have seen that whenever setup and hold violation time occurs, metastability occurs, so we have to see when signals violate this timing requirement:

• When the input signal is an asynchronous signal.
• When the clock skew/slew is too much (rise and fall time are more than the tolerable values).
• When interfacing two domains operating at two different frequencies or at the same frequency but with different phase.
• When the combinational delay is such that flip-flop data input changes in the critical window (setup+hold window)

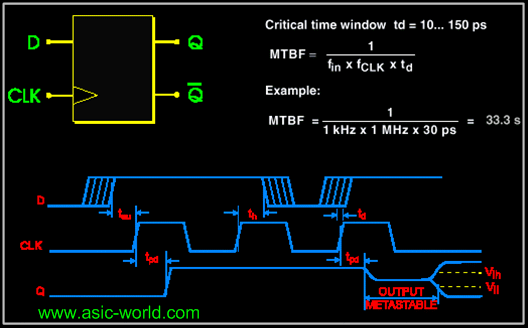
MTBF is Mean time between failure, what does that mean? Well MTBF gives us information on how often a particular element will fail or in other words, it gives the average time interval between two successive failures. The figure below shows a typical MTBF of a flip-flop and also it gives the MTBF equation. I am not looking here to derive MTBF equation :-)

In reality, one cannot avoid metastability and increased clock-to-Q delays in synchronizing asynchronous inputs, without the use of tricky self-timed circuits. So a more appropriate question might be "How do I tolerate metastability?"

In the simplest case, designers can tolerate metastability by making sure the clock period is long enough to allow for the resolution of quasi-stable states and for the delay of whatever logic may be in the path to the next flip-flop. This approach, while simple, is rarely practical given the performance requirements of most modern designs.

The most common way to tolerate metastability is to add one or more successive synchronizing flip-flops to the synchronizer. This approach allows for an entire clock period (except for the setup time of the second flip-flop) for metastable events in the first synchronizing flip-flop to resolve themselves. This does, however, increase the latency in the synchronous logic's observation of input changes.

Neither of these approaches can guarantee that metastability cannot pass through the synchronizer; they simply reduce the probability to practical levels.

In quantitative terms, if the Mean Time Between Failure (MTBF) of a particular flip-flop in the context of a given clock rate and input transition rate is 33.33 seconds then the MTBF of two such flip-flops used to synchronize the input would be (33.33* 33.33) = 18.514 Minutes. Well I have taken the worst flip-flop ever designed in history of man kind :-). The figure below shows how to connect two flip-flops in series to achieve this and also the resultant MTBF.

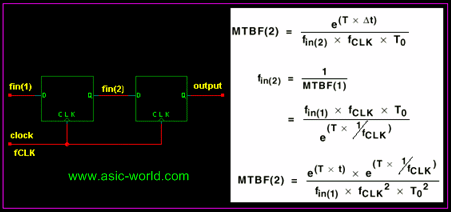Normally,

• We can use a metastable hardened flip-flop
• Cascade two or three D-Flip-Flops (two or three stages synchronizer).

• http://www-s.ti.com/sc/psheets/sdya006/sdya006.pdf
• Thomas J. Chaney, "Measured Flip-Flop Responses to Marginal Triggering", IEEE Transactions on Computers, Vol. C-32. No. 12, December 1983, pp.1207-1209.
• Lindsay Kleeman and Antonio Cantoni, "On the Unavoidability of Metastable Behavior in Digital Systems", IEEE Transactions on Computers, Vol. C-36. No. 1, January 1987, pp.109-112.
• Lindsay Kleeman and Antonio Cantoni, "Can Redundancy and Masking Improve the Performance of Synchronizers?", IEEE Transactions on Computers, Vol. C-35, No. 7, July 1986, pp.643-646.
• Cypress Semiconductor, "Are Your PLDs Metastable?, Fax ID: 6403, May 1992, Revised March 6,1997. http://www.cypress.com/pld/pldappnotes.html#pldmeta
• http://www.xilinx.com/apps/xapp.htm
• M. Valencia, M. J. Bellido, J. L. Huertas, A. J. Acosta, and S. Sanchez-Solano, "Modular Asynchronous Arbiter Insensitive to Metastability. IEEE Transactions on Computers, 44(12):1456-1461, December 1995.

Copyright © 1998-2014

Deepak Kumar Tala - All rights reserved

Do you have any Comment? mail me at:deepak@asic-world.com