| |
|

|
|
|
|
| |
|

|
| |
 |
Numbering System
|
|
|
Many number systems are in use in digital technology. The most common are the decimal, binary, octal, and hexadecimal systems. The decimal system is clearly the most familiar to us because it is a tool that we use every day. Examining some of its characteristics will help us to better understand the other systems. In the next few pages we shall introduce four numerical representation systems that are used in the digital system. There are other systems, which we will look at briefly. |
|
|
- Decimal
- Binary
- Octal
- Hexadecimal
|
| |
|

|
| |
 |
Decimal System
|
|
|
The decimal system is composed of 10 numerals or symbols. These 10 symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Using these symbols as digits of a number, we can express any quantity. The decimal system is also called the base-10 system because it has 10 digits. |
| |
|

|
|
|
|
103
|
102
|
101
|
100
|
|
10-1
|
10-2
|
10-3
|
|
=1000
|
=100
|
=10
|
=1
|
.
|
=0.1
|
=0.01
|
=0.001
|
|
Most Significant Digit
|
|
|
|
Decimal point
|
|
|
Least Significant Digit
|
|
| |
|

|
|
|
Even though the decimal system has only 10 symbols, any number of any magnitude can be expressed by using our system of positional weighting. |
| |
|

|
| |
 |
Decimal Examples
|
| |
|

|
|
|
- 3.1410
- 5210
- 102410
- 6400010
|
| |
|

|
| |
 |
Binary System
|
|
|
In the binary system, there are only two symbols or possible digit values, 0 and 1. This base-2 system can be used to represent any quantity that can be represented in decimal or other base system. |
| |
|

|
|
|
|
23
|
22
|
21
|
20
|
|
2-1
|
2-2
|
2-3
|
|
=8
|
=4
|
=2
|
=1
|
.
|
=0.5
|
=0.25
|
=0.125
|
|
Most Significant Digit
|
|
|
|
Binary point
|
|
|
Least Significant Digit
|
|
| |
|

|
| |
 |
Binary Counting
|
|
|
The Binary counting sequence is shown in the table: |
| |
|

|
|
|
|
23
|
22
|
21
|
20
|
Decimal
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
1
|
1
|
|
0
|
0
|
1
|
0
|
2
|
|
0
|
0
|
1
|
1
|
3
|
|
0
|
1
|
0
|
0
|
4
|
|
0
|
1
|
0
|
1
|
5
|
|
0
|
1
|
1
|
0
|
6
|
|
0
|
1
|
1
|
1
|
7
|
|
1
|
0
|
0
|
0
|
8
|
|
1
|
0
|
0
|
1
|
9
|
|
1
|
0
|
1
|
0
|
10
|
|
1
|
0
|
1
|
1
|
11
|
|
1
|
1
|
0
|
0
|
12
|
|
1
|
1
|
0
|
1
|
13
|
|
1
|
1
|
1
|
0
|
14
|
|
1
|
1
|
1
|
1
|
15
|
|
| |
|

|
|
|
|
| |
|

|
| |
 |
Representing Binary Quantities
|
|
|
In digital systems the information that is being processed is usually presented in binary form. Binary quantities can be represented by any device that has only two operating states or possible conditions. E.g.. a switch is only open or closed. We arbitrarily (as we define them) let an open switch represent binary 0 and a closed switch represent binary 1. Thus we can represent any binary number by using series of switches. |
| |
|

|
| |
 |
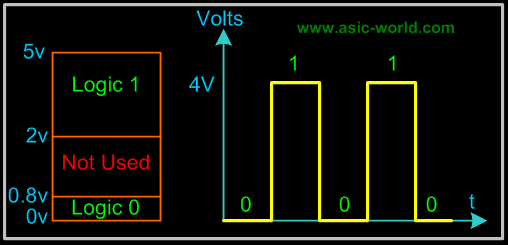
Typical Voltage Assignment
|
|
|
Binary 1: Any voltage between 2V to 5V |
|
|
Binary 0: Any voltage between 0V to 0.8V |
|
|
Not used: Voltage between 0.8V to 2V in 5 Volt CMOS and TTL Logic, this may cause error in a digital circuit. Today's digital circuits works at 1.8 volts, so this statement may not hold true for all logic circuits. |
| |
|

|
|
|
 |
| |
|

|
|
|
We can see another significant difference between digital and analog systems. In digital systems, the exact voltage value is not important; eg, a voltage of 3.6V means the same as a voltage of 4.3V. In analog systems, the exact voltage value is important. |
| |
|

|
|
|
The binary number system is the most important one in digital systems, but several others are also important. The decimal system is important because it is universally used to represent quantities outside a digital system. This means that there will be situations where decimal values have to be converted to binary values before they are entered into the digital system. |
| |
|

|
|
|
In additional to binary and decimal, two other number systems find wide-spread applications in digital systems. The octal (base-8) and hexadecimal (base-16) number systems are both used for the same purpose- to provide an efficient means for representing large binary system. |
| |
|

|
| |
 |
Octal System
|
|
|
The octal number system has a base of eight, meaning that it has eight possible digits: 0,1,2,3,4,5,6,7. |
| |
|

|
|
|
|
83
|
82
|
81
|
80
|
|
8-1
|
8-2
|
8-3
|
|
=512
|
=64
|
=8
|
=1
|
.
|
=1/8
|
=1/64
|
=1/512
|
|
Most Significant Digit
|
|
|
|
Octal point
|
|
|
Least Significant Digit
|
|
| |
|

|
| |
 |
Octal to Decimal Conversion
|
| |
|

|
|
|
- 2378 = 2 x (82) + 3 x (81) + 7 x (80) = 15910
- 24.68 = 2 x (81) + 4 x (80) + 6 x (8-1) = 20.7510
- 11.18 = 1 x (81) + 1 x (80) + 1 x (8-1) = 9.12510
- 12.38 = 1 x (81) + 2 x (80) + 3 x (8-1) = 10.37510
|
| |
|

|
| |
 |
Hexadecimal System
|
|
|
The hexadecimal system uses base 16. Thus, it has 16 possible digit symbols. It uses the digits 0 through 9 plus the letters A, B, C, D, E, and F as the 16 digit symbols. |
| |
|

|
|
|
|
163
|
162
|
161
|
160
|
|
16-1
|
16-2
|
16-3
|
|
=4096
|
=256
|
=16
|
=1
|
.
|
=1/16
|
=1/256
|
=1/4096
|
|
Most Significant Digit
|
|
|
|
Hexa Decimal point
|
|
|
Least Significant Digit
|
|
| |
|

|
| |
 |
Hexadecimal to Decimal Conversion
|
| |
|

|
|
|
- 24.616 = 2 x (161) + 4 x (160) + 6 x (16-1) = 36.37510
- 11.116 = 1 x (161) + 1 x (160) + 1 x (16-1) = 17.062510
- 12.316 = 1 x (161) + 2 x (160) + 3 x (16-1) = 18.187510
|
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|