| |
|

|
|
|
|
| |
|

|
| |
 |
Encoders
|
|
|
An encoder is a combinational circuit that performs the inverse operation of a decoder. If a device output code has fewer bits than the input code has, the device is usually called an encoder. e.g. 2n-to-n, priority encoders. |
| |
|

|
|
|
The simplest encoder is a 2n-to-n binary encoder, where it has only one of 2n inputs = 1 and the output is the n-bit binary number corresponding to the active input. |
| |
|

|
|
|
 |
| |
|

|
| |
 |
Example - Octal-to-Binary Encoder
|
|
|
Octal-to-Binary take 8 inputs and provides 3 outputs, thus doing the opposite of what the 3-to-8 decoder does. At any one time, only one input line has a value of 1. The figure below shows the truth table of an Octal-to-binary encoder. |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
I0
|
I1
|
I2
|
I3
|
I4
|
I5
|
I6
|
I7
|
Y2
|
Y1
|
Y0
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
|
| |
|

|
|
|
For an 8-to-3 binary encoder with inputs I0-I7 the logic expressions of the outputs Y0-Y2 are: |
| |
|

|
|
|
Y0 = I1 + I3 + I5 + I7 |
|
|
Y1= I2 + I3 + I6 + I7 |
|
|
Y2 = I4 + I5 + I6 +I7 |
| |
|

|
|
|
Based on the above equations, we can draw the circuit as shown below |
| |
|

|
|
|
Circuit |
| |
|

|
|
|
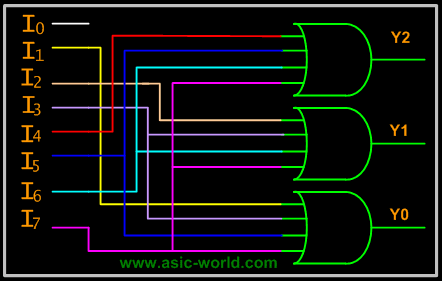 |
| |
|

|
|
|
|
| |
|

|
| |
 |
Example - Decimal-to-Binary Encoder
|
|
|
Decimal-to-Binary take 10 inputs and provides 4 outputs, thus doing the opposite of what the 4-to-10 decoder does. At any one time, only one input line has a value of 1. The figure below shows the truth table of a Decimal-to-binary encoder. |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
I0
|
I1
|
I2
|
I3
|
I4
|
I5
|
I6
|
I7
|
I8
|
I9
|
Y3
|
Y2
|
Y1
|
Y0
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
|
| |
|

|
|
|
From the above truth table , we can derive the functions Y3, Y2, Y1 and Y0 as given below. |
| |
|

|
|
|
Y3 = I8 + I9 |
|
|
Y2 = I4 + I5 + I6 + I7 |
|
|
Y1 = I2 + I3 + I6 + I7 |
|
|
Y0 = I1 + I3 + I5 + I7 + I9 |
| |
|

|
| |
 |
Priority Encoder
|
|
|
If we look carefully at the Encoder circuits that we got, we see the following limitations. If more then two inputs are active simultaneously, the output is unpredictable or rather it is not what we expect it to be. |
| |
|

|
|
|
This ambiguity is resolved if priority is established so that only one input is encoded, no matter how many inputs are active at a given point of time. |
| |
|

|
|
|
The priority encoder includes a priority function. The operation of the priority encoder is such that if two or more inputs are active at the same time, the input having the highest priority will take precedence. |
| |
|

|
| |
 |
Example - 4to3 Priority Encoder
|
|
|
The truth table of a 4-input priority encoder is as shown below. The input D3 has the highest priority, D2 has next highest priority, D0 has the lowest priority. This means output Y2 and Y1 are 0 only when none of the inputs D1, D2, D3 are high and only D0 is high. |
| |
|

|
|
|
A 4 to 3 encoder consists of four inputs and three outputs, truth table and symbols of which is shown below. |
| |
|

|
|
|
Truth Table |
| |
|

|
|
|
|
D3
|
D2
|
D1
|
D0
|
Y2
|
Y1
|
Y0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
0
|
0
|
1
|
x
|
0
|
1
|
0
|
|
0
|
1
|
x
|
x
|
0
|
1
|
1
|
|
1
|
x
|
x
|
x
|
1
|
0
|
0
|
|
| |
|

|
|
|
Now that we have the truth table, we can draw the Kmaps as shown below. |
| |
|

|
|
|
Kmaps |
| |
|

|
|
|
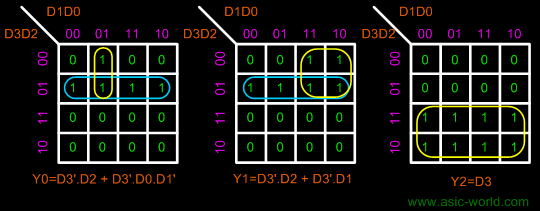 |
| |
|

|
|
|
From the Kmap we can draw the circuit as shown below. For Y2, we connect directly to D3. |
| |
|

|
|
|
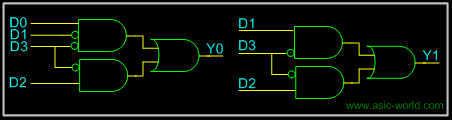 |
| |
|

|
|
|
We can apply the same logic to get higher order priority encoders. |
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|