| |
|

|
|
|
|
| |
|

|
| |
 |
n-bit Carry Ripple Adder
|
|
|
An n-bit adder used to add two n-bit binary numbers can be built by connecting n full adders in series. Each full adder represents a bit position j (from 0 to n-1). |
| |
|

|
|
|
Each carry out C-out from a full adder at position j is connected to the carry in C-in of the full adder at higher position j+1. The output of a full adder at position j is given by: Sj= Xj  Yj Yj  Cj Cj |
| |
|

|
|
|
Cj+1 = Xj . Yj + Xj . Cj + Y . Cj |
| |
|

|
|
|
In the expression of the sum Cj must be generated by the full adder at lower position j. The propagation delay in each full adder to produce the carry is equal to two gate delays = 2 D Since the generation of the sum requires the propagation of the carry from the lowest position to the highest position , the total propagation delay of the adder is approximately: |
| |
|

|
|
|
Total Propagation delay = 2 nD |
| |
|

|
| |
 |
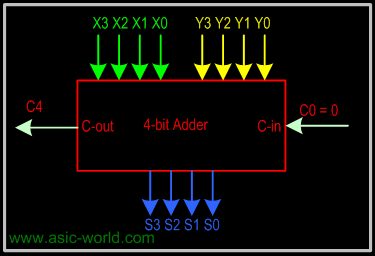
4-bit Carry Ripple Adder
|
| |
|

|
|
|
Adds two 4-bit numbers: |
| |
|

|
|
|
X = X3 X2 X1 X0 |
|
|
Y = Y3 Y2 Y1 Y0 |
| |
|

|
|
|
producing the sum S = S3 S2 S1 S0 , C-out = C4 from the most significant position j=3 |
| |
|

|
|
|
Total Propagation delay = 2 nD = 8D or 8 gate delays |
| |
|

|
|
|
 |
| |
|

|
|
|
|
| |
|

|
| |
 |
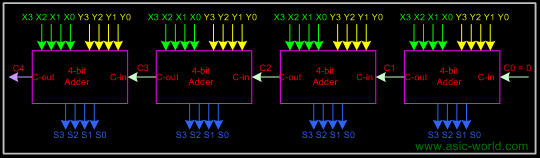
Larger Adder
|
|
|
Example: 16-bit adder using 4 4-bit adders. Adds two 16-bit inputs X (bits X0 to X15), Y (bits Y0 to Y15) producing a 16-bit Sum S (bits S0 to S15) and a carry out C16 from the most significant position. |
| |
|

|
|
|
 |
| |
|

|
|
|
Propagation delay for 16-bit adder = 4 x propagation delay of 4-bit adder |
|
|
= 4 x 2 nD = 4 x 8D = 32 D |
|
|
or 32 gate delays |
| |
|

|
| |
 |
Carry Look-Ahead Adder
|
|
|
The delay generated by an N-bit adder is proportional to the length N of the two numbers X and Y that are added because the carry signals have to propagate from one full-adder to the next. For large values of N, the delay becomes unacceptably large so that a special solution needs to be adopted to accelerate the calculation of the carry bits. This solution involves a "look-ahead carry generator" which is a block that simultaneously calculates all the carry bits involved. Once these bits are available to the rest of the circuit, each individual three-bit addition (Xi+Yi+carry-ini) is implemented by a simple 3-input XOR gate. The design of the look-ahead carry generator involves two Boolean functions named Generate and Propagate. For each input bits pair these functions are defined as: |
| |
|

|
|
|
Gi = Xi . Yi |
|
|
Pi = Xi + Yi |
| |
|

|
|
|
The carry bit c-out(i) generated when adding two bits Xi and Yi is '1' if the corresponding function Gi is '1' or if the c-out(i-1)='1' and the function Pi = '1' simultaneously. In the first case, the carry bit is activated by the local conditions (the values of Xi and Yi). In the second, the carry bit is received from the less significant elementary addition and is propagated further to the more significant elementary addition. Therefore, the carry_out bit corresponding to a pair of bits Xi and Yi is calculated according to the equation: |
| |
|

|
|
|
carry_out(i) = Gi + Pi.carry_in(i-1) |
| |
|

|
|
|
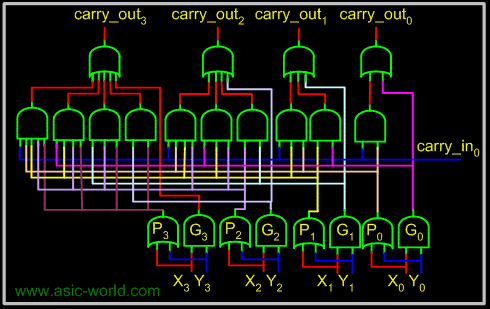
For a four-bit adder the carry-outs are calculated as follows |
| |
|

|
|
|
carry_out0 = G0 + P0 . carry_in0 |
|
|
carry_out1 = G1 + P1 . carry_out0 = G1 + P1G0 + P1P0 . carry_in0 |
|
|
carry_out2 = G2 + P2G1 + P2P1G0 + P2P1P0 . carry_in0 |
|
|
carry_out3 = G3 + P3G2 + P3P2G1 + P3P2P1G0 + P3P2P1 . carry_in0 |
| |
|

|
| |
|

|
|
|
The set of equations above are implemented by the circuit below and a complete adder with a look-ahead carry generator is next. The input signals need to propagate through a maximum of 4 logic gate in such an adder as opposed to 8 and 12 logic gates in its counterparts illustrated earlier. |
| |
|

|
|
|
 |
| |
|

|
|
|
Sums can be calculated from the following equations, where carry_out is taken from the carry calculated in the above circuit. |
| |
|

|
|
|
sum_out0 = X 0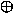 Y0 Y0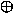 carry_out0 carry_out0 |
|
|
sum_out1 = X 1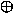 Y1 Y1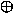 carry_out1 carry_out1 |
|
|
sum_out2 = X 2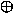 Y2 Y2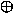 carry_out2 carry_out2 |
|
|
sum_out3 = X 3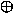 Y3 Y3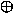 carry_out3 carry_out3 |
| |
|

|
|
|
 |
| |
|

|
| |
 |
BCD Adder
|
|
|
BCD addition is the same as binary addition with a bit of variation: whenever a sum is greater than 1001, it is not a valid BCD number, so we add 0110 to it, to do the correction. This will produce a carry, which is added to the next BCD position. |
| |
|

|
|
|
- Add the two 4-bit BCD code inputs.
- Determine if the sum of this addition is greater than 1001; if yes, then add 0110 to this sum and generate a carry to the next decimal position.
|
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|